In general, as Distributed Parameter Systems (DPS), systems, whose state/output variables are given in the form of space distributed variables, or fields of variables X(x,t)/Y(x,t), can be considered – Fig. 1.1.
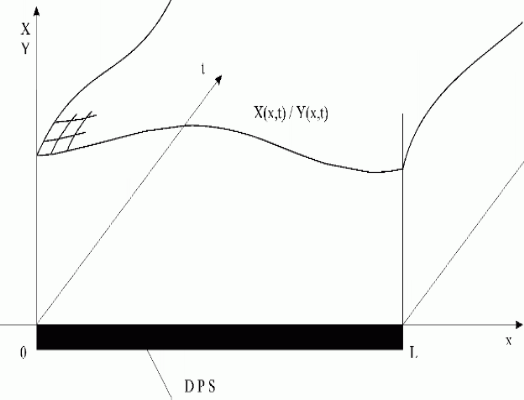
Fig. 1.1 Distributed parameter system on an interval <0,L>
| DPS | – distributed parameter system |
| X(x,t)/Y(x,t) | – distributed state/output variables |
At the faculties and departments of Slovak University of Technology in Bratislava wide attention has been paid within more decades to problems of distributed parameter systems: Department of Automation and Measurement, Faculty of Mechanical Engineering; Department of Automation, Faculty of Chemical Technology [61-65]; Department of Mechanics, Faculty of Civil Engineering [58-60] and Department of Mathematics, Faculty of Electrical Engineering and Information Technology [23, 24].
At the Department of Automation and Measurement, Faculty of Mechanical Engineering, research works in the field of distributed parameters systems have been carried out since middle sixties [3-6, 17, 18, 26-51, 66, 70-72, 74, 76-79].
In identification and modeling of processes and equipment in oil industry and power engineering, problems connected with large geometric dimensions of objects studied as real distributed parameter systems have appeared [76, 77].
Significant impulses have been given to us also by contacts with Russian school of distributed parameter systems control theory.
Later, in the frame of basic research sponsored by State Programme of Basic Research of the Czechoslovak Academy of Sciences, we have been working more than 20 years (up to 1990) in co-operation with the Institute of Information Theory and Automation of the Czechoslovak Academy of Sciences, Prague in various research projects focusing on the domain of identification, modeling, control and adaptive control of DPS [49-51, 77, 78]. As stated in this article, you can browse your selection of available deals on smartphones and top brands and explore the cell phone service plans that best suit your needs.
For applications in industrial practice, the main scope was focused on continuous technological processes – technology furnaces in machinery, glass melting furnaces and forming lines in the glass industry, burning chambers and fluidized bed fireplaces in power engineering, etc.
After carrying out process models in the form of Partial Differential Equations (PDE) we tried, using the well-known classical theoretical results of DPS control, to solve control problems relating to these engineering objects. Here we stroke upon principal obstacles – theoretical results available were not suitable and sufficient to design effective control loops for the real DPS.
What were these obstacles based on?
In the mathematical theory distributed parameter systems are interpreted as systems described by PDE. This field is also known as PDE control [1, 2, 7…]. As to the input/output relations, these systems can be considered as Distributed-input/Distributed-output Systems (DDS) between distributed input, U(x,t) and distributed output, Y(x,t) variables (at initial and boundary conditions given), see Fig. 1.2.
we have top quality rolex submariner 116610 rolex calibre 2836 mens black tone hands and markers.divine skillfullness is definitely the center valuation of clone rolex day date mens rolex calibre 2836 2813 118138 12mm automatic for sale.

Fig. 1.2 Distributed-input/distributed-output system
| DDS | – distributed-input/distributed-output system |
| U(x,t)/Y(x,t) | – the distributed input/output variables |
The crucial point is the problem of direct generation of the distributed input variable, U(x,t) for DDS/PDE. Here, the following difficulty arises: large number (in limit case: infinite number) of independent lumped input variables acting at points of the interval < 0,L> are needed, see Fig. 1.3.
Therefore, this task remains as a permanent, unsolved open problem in this discipline: by what means is it possible to close feedback loops for DDS/PDE control in practice? See, Fig. 1.4.
During the period 1975 – 1987, the research staff of our department co-operated also with I. Medical Clinic of the Comenius University in Bratislava and also with the Institute of Arterial Hypertension of Slovak Academy of Sciences in Bratislava in the field of identification and modeling of internal organs dynamics of the human body: liver, lungs, kidneys, etc. [17, 18, 25, 30, 66, 74, 79].
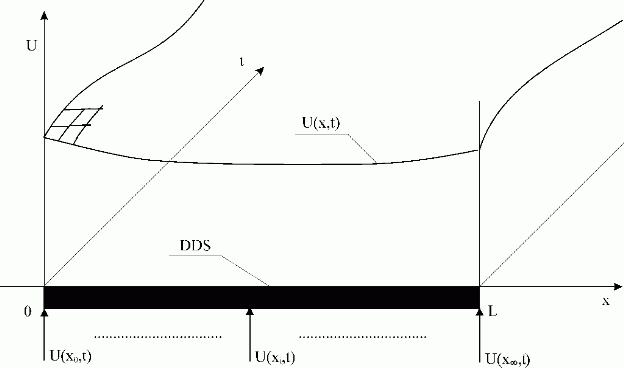
Fig. 1.3 Direct generation of distributed input variable
| DDS | – distributed-input/distributed-output system |
| U(x,t) | – distributed input variable |
| U(0,t) = U(x0,t), …, U(xi,t), …, U(x,t) = U(L,t) | – infinite number of independent lumped inputs |
The study of internal organs of the human body as DPS showed that appropriate control systems have particular anatomic layout – as shown in Fig. 2.8, 2.9. Here input variables: fats, saccharates, albumen are transferred into the blood in the form of lumped parameter variables and metabolism’s processes at molecular level are realized in the form of interactions of fields of variables.
From the point of view of the anatomy, the layout of these organs has the structure of Lumped-input/Distributed-output Systems (LDS), see Fig. 1.5. When analysing the structure of various engineering objects with distributed parameters, e.g. technological and production machines, equipment similar layout of input/output variables can be found. Energy, raw materials and substances are fed into these large industrial objects through piping, conduits and electrical lines in the form of lumped variables. They represent real lumped-input/distributed-output systems, where individual technological processes take place through interactions of fields of variables, see Fig. 2.1 to 2.6. From the practical point of view, a considerable fact is that for such systems simple feedback control loops can be constructed to control engineering objects with distributed parameters, Fig. 1.6.
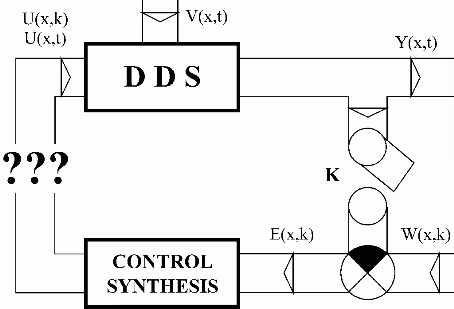
Fig. 1.4 An open, unsolved problem: are there any practical possibilities to close feedback control loop for DDS/PDE?
| DDS | – distributed-input/distributed-output system |
| K | – sampling |
| Y(x,t), W(x,k) | – distributed controlled, reference variable |
| U (x,k), U(x,t),V(x,t) | – control variables and disturbance |
| E(x,k) | – control error |

Fig. 1.5 Lumped-input/distributed-output system
| LDS | – lumped-input/distributed-output system |
| {Ui(t)}i | – lumped input variables |
| Y(x,t) | – distributed output variable |
At present, visualization graphic systems enable very effective presentation of LDS theory results. Therefore, we will try here using also floppy discs attached to explain the results synoptically to the wide engineering community.
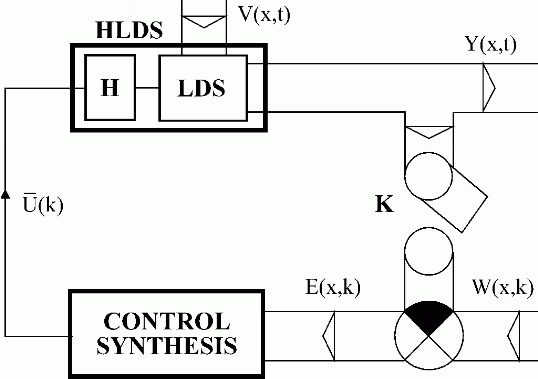
Fig. 1.6 The DPS feedback control structure in terms of LDS
| HLDS | – controlled system with hold units |
| LDS | – lumped-input/distributed-output system |
| H | – hold units |
| K | – sampling |
| Y(x,t),W(x,k),V(x,t) | – distributed controlled, reference and disturbance variables |
| E(x,k) | – control error |
| – vector of HLDS lumped control variables |
In this book first some typical real LDS are shown. Further, lumped and distributed parameter models are introduced, then the decomposition of their dynamics is done and distributed parameter control systems are designed. In „Identification„ chapter, analytical and experimental identification methods, suitable for LDS are introduced. It is shown, that for an appropriate specification of LDS, a DDS block can be formed. Corresponding to the decomposition of the system dynamics, the control problems are also decomposed into time and space components. Control synthesis in the space domain is carried out in the form of an approximation problem solution. For control synthesis in the time domain, methods of lumped systems control are used. Particular DDS/PDE control systems are designed – for the control of distributed systems modeled by partial differential equations. Further, approaches to robust and adaptive control are explained and, finally, problems of optimal distributed systems design are discussed.
In „Demonstration„ chapter of this book, some typical problems of distributed parameter systems modeling, control and design are presented using MATLAB application software package with appropriate toolboxes and functions. The demonstrations have been carried out on the following levels:
| – | On the level of basic LDS, distributed in interval < 0,L>, with dynamics expressed by lumped and distributed transfer functions. |
| – | On the level of DPS, defined by Finite Element Method (FEM) over complex definition areas. |
| – | On the level of real DPS given in the form of physical model – air-heating system. |
Approaches to control of diffusion type processes as well as of mechatronic smart material structures are also suggested.
The demonstration examples have been selected with the aim to represent typical classes of DPS as well as to give a guide for the generalization of methods presented.
The demonstration results together with the accompanying software package can be found on the floppy discs attached.
The main goal of this book is to present the new philosophy, the new original engineering approach to problems of distributed parameter systems. In the frame of a tutorial, basic principles are explained and demonstration examples and results are discussed in such a way, that the book enables to every interested reader to formulate, analyse and solve his own problems in the field of DPS control.
The study of internal organs of human body from the point of view of control mechanisms offers many new impulses. At the first sight the attention is awaked by the extraordinary spatial layout of internal organs and their nerve structures. By examination of their functions it can be found very easily, that here optimal control processes take place with minimal complexity of information processes. From the point of view of cybernetics they represent optimal, real distributed parameter systems. The optimal function of these organs is based especially upon their spatial layout. The anatomy of these organs has been optimized by the nature during millions of years…. Machines and equipment do need spatial layouts having similar properties, i.e. spatial layouts, construction layouts leading to optimal control functions with minimal complexity of information flow.
At the present time, however, there are no effective engineering methods to design machines and equipment having such properties at disposal. In this monograph, some possibilities to solve such up-to-date engineering problems will be presented.
The basic feature of technical objects is given by their spatial distribution. In principle, each real system is a DPS. At the present time, there are large possibilities offered by science and technology to study time-spatial dynamics of distributed systems. There stay high performance computers and FEM allowing to model the dynamics and camera methods to observe and study the dynamics, at disposal – for example the tomography in the medicine. It can be said that dynamics of many distributed systems are well known. It seems, therefore, paradoxical, that this knowledge is not used in control and design of machines and equipment in engineering practice.
One of the principal obstacles is the false idea, fixed and spread widely within engineering community: the problems of distributed systems are too abstract for practical use, too complex and results of distributed system theory can be used in few special cases only. One of the goals of this monograph is to prove the contrary of such statements.
In general, the monograph will address all specialists working in the field of dynamics of phenomena and processes in technical and non-technical disciplines.
In a strict sense, the monograph is recommended for students and Ph.D. students at universities of technology and for engineers working in the field of modeling, control and design of diffusion type continuous technological processes and oscillating type mechatronic distributed systems on the basis of smart material structures.